Fractal Music

Music Theory Background

Ancient Greek roots of the Western tonal system

From the time of Pythagoras in the 6th century B.C., the ancients Greeks were fascinated by the integer relationships between the tones of the harmonic series. They noticed that certain pairs of these tones, when played simultaneously, sounded more pleasing than others. These pleasing combinations are referred to as consonant.

Perfect Fifth (more consonant) Major Second (less consonant)

They devised various means for arranging the pitches of the seven most consonant tones (those that best complemented each other) to occupy the same octave and thereby constructed a scale. The notes obtained in this fashion are named according the first seven letters of the alphabet. Because they represent integer relationships, each note in the scale can be defined relative to any starting note, or tonic, by a simple ratio. Here is an example of a harmonically derived scale showing the ratios between adjacent notes. 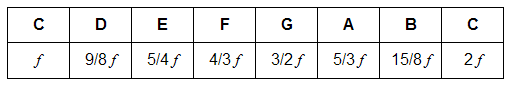C Major Scale The smallest distance between adjacent notes is called a semitone or half step. There are 12 semitones in an octave. A whole tone is equal to two semitones. The collection of all twelve notes in the octave, played in sequence is called the chromatic scale. Chromatic Scale

Return to music theory.